Structural eqution modelling (SEM)
Combining Path models and CFA to create structural equation models (SEM) allows researchers to combine allow for measurment imperfection whilst also (attempting to) infer information about causation.
SEM involves adding paths to CFA models which are, like predictors in standard regression models, are assumed to be causal in nature; i.e. rather than variables \(x\) and \(y\) simply covarying with one another, we are prepared to make the assumption that \(x\) causes \(y\).
It’s worth pointing out though, right from the offset, that causal relationships drawn from SEM models always dependent on assumptions we are prepared to make when setting up our model. There is nothing magical in the technique that makes allows us to infer causality from non-experimental data (although note SEM can be used for some experimental analyses).
It is only be our substantive knowledge of the domain that makes any kind of causal inference reasonable, and when using SEM the onus is always on us to check our assumptions, provide sensitivity analyses which test alternative causal models, and interpret observational data cautiously.
[Note, there are techniques which use SEM as a means to make stronger kinds of causal statements, for example instrumental variable analysis, but even here, inferring causality still requires that we make strong assumptions about the process which generated our data.
Nonetheless, with these caveats in mind, SEM can be a useful technique to quantify relationships been observed variables where we have measurement error, and especially where we have a theoretical model linking these observations.
Steps to running an SEM
Identify and test the fit of a measurement model. This is a CFA model which includes all of your observed variables, arranged in relation to the latent variables you think generated the data, and where covariances between all these latent variables are included. This step many include many rounds of model fitting and modification.
Ensure your measurement model fits the data adequately before continuing. Test alternative or simplified measurements models and report where these perform well (e.g. are close in fit to your desired model). SEM models that are based on a poorly fitting measurment model will produce parameter estimates that are imprecise, unstable or both, and you should not proceed unless an adequately fitting measrement model is founds (see this nice discussion, which includes relevant references).
Convert your measurement model by removing covariances between latent variables where necessary and including new structural paths. Test model fit, and interpret the paths of interest. Avoid making changes to the measurement part of the model at this stage. Where the model is complex consider adjusting p values to allow for multuple comparisons (if using NHST).
Test alternative models (e.g. with paths removed or reversed). Report where alternatives also fit the data.
In writing up, provide sufficient detail for other researchers to replicate your analyses, and to follow the logic of the ammendments you make. Ideally share your raw data, but at a minimum share the covariance matrix. Report GOF statistics, and follow published reporting guidelines for SEM [@schreiber_reporting_2006]. Always include a diagram of your final model (at the very least).
A worked example: Building from a measurement model to SEM
Imagine we have some data from a study that aimed to test the theory of planned behaviour. Researcher measured exercise and intentions, along with multiple measures of attitudes, social norms and percieved behavioural control.
tpb.df %>% psych::describe(fast=T)| vars | n | mean | sd | min | max | range | se |
| 1 | 469 | -0.00539 | 1.61 | -5.99 | 4.78 | 10.8 | 0.0745 |
| 2 | 459 | 0.117 | 1.22 | -3.17 | 4.18 | 7.35 | 0.057 |
| 3 | 487 | -0.001 | 1.08 | -3.22 | 3.13 | 6.35 | 0.0487 |
| 4 | 487 | 0.078 | 1.53 | -5.04 | 5.43 | 10.5 | 0.0695 |
| 5 | 487 | 0.0376 | 1.22 | -3.76 | 3.61 | 7.37 | 0.0551 |
| 6 | 487 | 0.00863 | 1.11 | -3.21 | 3.11 | 6.33 | 0.0501 |
| 7 | 471 | 0.0261 | 1.1 | -2.94 | 3.14 | 6.08 | 0.0506 |
| 8 | 487 | -0.00329 | 1.35 | -4.13 | 4.03 | 8.16 | 0.061 |
| 9 | 487 | -0.0865 | 1.31 | -4.86 | 4.08 | 8.94 | 0.0593 |
| 10 | 487 | -0.00563 | 1.19 | -3.12 | 3.34 | 6.46 | 0.0537 |
| 11 | 487 | -0.0863 | 1.06 | -3.23 | 3.34 | 6.57 | 0.0481 |
| 12 | 487 | -0.0663 | 1.16 | -4.11 | 3.5 | 7.61 | 0.0525 |
| 13 | 469 | 10.1 | 2.55 | 1.83 | 16.7 | 14.9 | 0.118 |
| 14 | 487 | 80.2 | 18.8 | 15 | 138 | 123 | 0.851 |
There were some missing data, but nothing to suggest a systematic pattern. For the moment we continue with standard methods:
mice::md.pattern(tpb.df)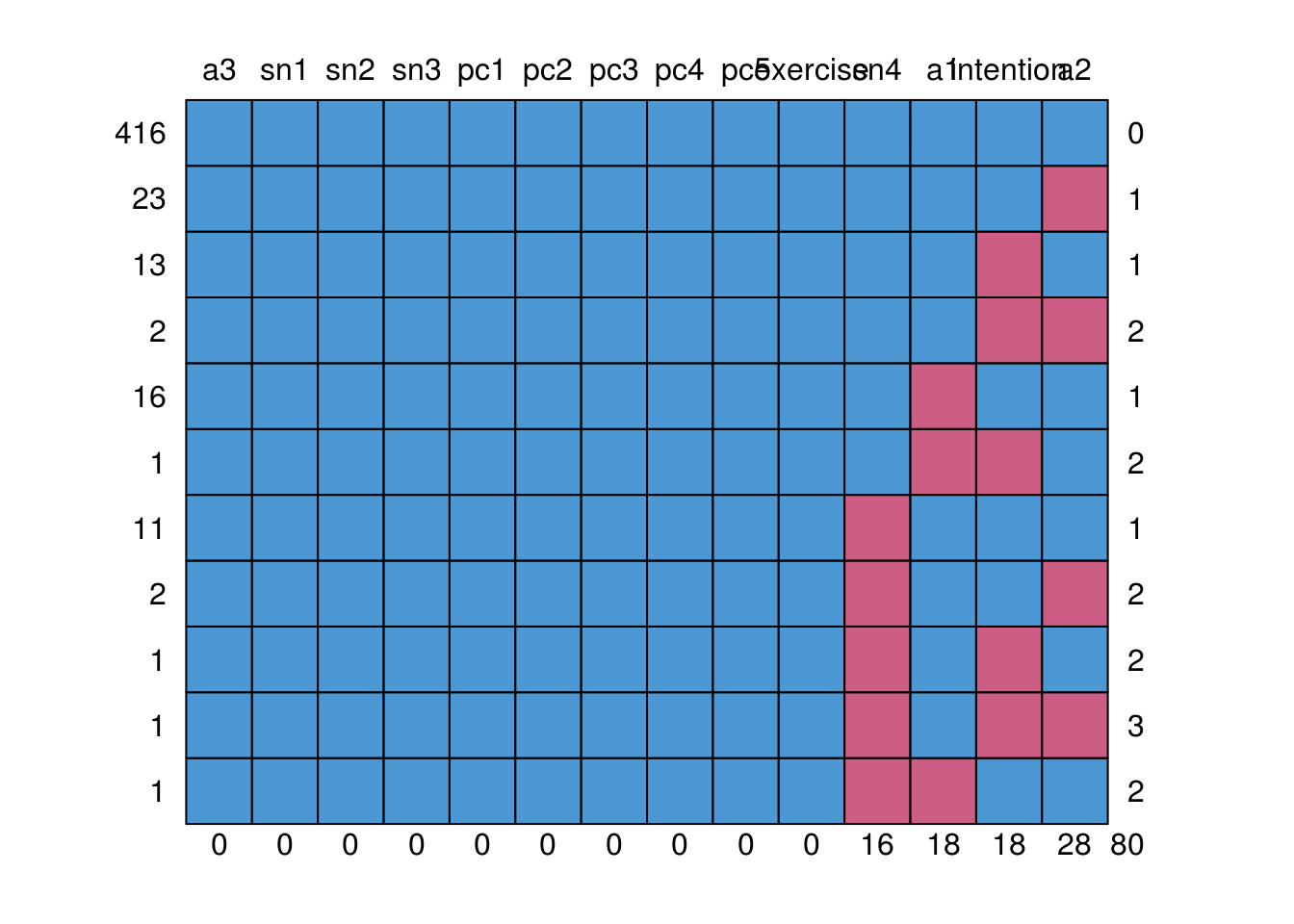
a3 sn1 sn2 sn3 pc1 pc2 pc3 pc4 pc5 exercise sn4 a1 intention a2
416 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
23 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1
13 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1
2 1 1 1 1 1 1 1 1 1 1 1 1 0 0 2
16 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 2
11 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
2 1 1 1 1 1 1 1 1 1 1 0 1 1 0 2
1 1 1 1 1 1 1 1 1 1 1 0 1 0 1 2
1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 3
1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 2
0 0 0 0 0 0 0 0 0 0 16 18 18 28 80We start by fitting a measurement model. The model sytax includes lines with
=~separatatig left and right hand side (to define the latent variables)~~to specify latent covariances
We are not including exercise and intention yet because these are observed
variables only (we don’t have multiple measurements for them) and so they don’t
need to be in the measurement model:
mes.mod <- '
# the "measurement" part, defining the latent variables
AT =~ a1 + a2 + a3 + sn1
SN =~ sn1 + sn2 + sn3 + sn4
PBC =~ pc1 + pc2 + pc3 + pc4 + pc5
# note that lavaan automatically includes latent covariances
# but we can add here anyway to be explicit
AT ~~ SN
SN ~~ PBC
AT ~~ PBC
'We can fit this model to the data like so:
mes.mod.fit <- cfa(mes.mod, data=tpb.df)
summary(mes.mod.fit)
lavaan 0.6-3 ended normally after 52 iterations
Optimization method NLMINB
Number of free parameters 28
Used Total
Number of observations 429 487
Estimator ML
Model Fit Test Statistic 50.290
Degrees of freedom 50
P-value (Chi-square) 0.462
Parameter Estimates:
Information Expected
Information saturated (h1) model Structured
Standard Errors Standard
Latent Variables:
Estimate Std.Err z-value P(>|z|)
AT =~
a1 1.000
a2 0.471 0.056 8.466 0.000
a3 0.239 0.042 5.654 0.000
sn1 -0.145 0.223 -0.651 0.515
SN =~
sn1 1.000
sn2 0.529 0.153 3.456 0.001
sn3 0.294 0.089 3.300 0.001
sn4 0.335 0.099 3.383 0.001
PBC =~
pc1 1.000
pc2 0.860 0.098 8.813 0.000
pc3 0.647 0.081 7.978 0.000
pc4 0.425 0.069 6.133 0.000
pc5 0.643 0.081 7.964 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
AT ~~
SN 1.488 0.460 3.233 0.001
SN ~~
PBC 0.045 0.085 0.525 0.600
AT ~~
PBC 0.010 0.086 0.116 0.908
Variances:
Estimate Std.Err z-value P(>|z|)
.a1 0.586 0.195 2.997 0.003
.a2 1.068 0.086 12.494 0.000
.a3 1.018 0.072 14.222 0.000
.sn1 0.870 0.239 3.640 0.000
.sn2 0.940 0.090 10.404 0.000
.sn3 1.071 0.077 13.887 0.000
.sn4 1.028 0.076 13.544 0.000
.pc1 0.871 0.104 8.401 0.000
.pc2 1.084 0.100 10.842 0.000
.pc3 1.018 0.082 12.431 0.000
.pc4 0.992 0.072 13.690 0.000
.pc5 1.014 0.081 12.447 0.000
AT 2.035 0.259 7.859 0.000
SN 1.873 0.882 2.124 0.034
PBC 0.888 0.135 6.600 0.000And we can assess model fit using fitmeasures. Here we select a subset of the
possible fit indices to keep the output manageable.
useful.fit.measures <- c('chisq', 'rmsea', 'cfi', 'aic')
fitmeasures(mes.mod.fit, useful.fit.measures)
chisq rmsea cfi aic
50.290 0.004 1.000 16045.276 This model looks pretty good (see the guide to fit indices), but still check modification indices to identify improvements. If they made theoretical sense we might choose to add paths:
modificationindices(mes.mod.fit) %>%
as_data_frame() %>%
filter(mi>4) %>%
arrange(-mi) %>%
pander(caption="Modification indices for the measurement model")| lhs | op | rhs | mi | epc | sepc.lv | sepc.all | sepc.nox |
|---|---|---|---|---|---|---|---|
| AT | =~ | sn2 | 20.39 | 0.5284 | 0.7536 | 0.6226 | 0.6226 |
| sn1 | ~~ | sn2 | 15.04 | -0.4689 | -0.4689 | -0.5184 | -0.5184 |
| AT | =~ | sn4 | 12.49 | -0.3035 | -0.4329 | -0.3891 | -0.3891 |
| a1 | ~~ | sn2 | 8.476 | 0.2457 | 0.2457 | 0.331 | 0.331 |
| sn1 | ~~ | sn4 | 6.54 | 0.216 | 0.216 | 0.2285 | 0.2285 |
| a2 | ~~ | pc5 | 4.098 | -0.1118 | -0.1118 | -0.1074 | -0.1074 |
However, in this case unless we had substantive reasons to add the paths, it would probably be reasonable to continue with the original model.
The measurement model fits, so proceed to SEM
Our SEM model adapts the CFA (measurement model), including additional observed variables (e.g. intention and exercise) and any relevant structural paths:
sem.mod <- '
# this section identical to measurement model
AT =~ a1 + a2 + a3 + sn1
SN =~ sn1 + sn2 + sn3 + sn4
PBC =~ pc1 + pc2 + pc3 + pc4 + pc5
# additional structural paths
intention ~ AT + SN + PBC
exercise ~ intention
'We can fit it as before, but now using the sem() function rather than the
cfa() function:
sem.mod.fit <- sem(sem.mod, data=tpb.df)The first thing we do is check the model fit:
fitmeasures(sem.mod.fit, useful.fit.measures)
chisq rmsea cfi aic
171.065 0.058 0.929 20638.124 RMSEA is slightly higher than we like, so we can check the modification indices:
sem.mi <- modificationindices(sem.mod.fit) %>%
as_data_frame() %>%
arrange(-mi)
sem.mi %>%
head(6) %>%
pander(caption="Top 6 modification indices for the SEM model")| lhs | op | rhs | mi | epc | sepc.lv | sepc.all | sepc.nox |
|---|---|---|---|---|---|---|---|
| exercise | ~ | PBC | 90.14 | 7.601 | 7.049 | 0.3695 | 0.3695 |
| PBC | ~ | exercise | 89.49 | 0.04938 | 0.05325 | 1.016 | 1.016 |
| intention | ~ | exercise | 47.03 | -0.1233 | -0.1233 | -0.9106 | -0.9106 |
| intention | ~~ | exercise | 47.03 | -16.18 | -16.18 | -0.6779 | -0.6779 |
| AT | =~ | sn2 | 16.14 | 0.5093 | 0.7043 | 0.5855 | 0.5855 |
| pc1 | ~~ | exercise | 15.08 | 2.405 | 2.405 | 0.2205 | 0.2205 |
Interestingly, this model suggests two additional paths involving exercise and
the PBC latent:
sem.mi %>%
filter(lhs %in% c('exercise', 'PBC') & rhs %in% c('exercise', 'PBC')) %>%
pander()| lhs | op | rhs | mi | epc | sepc.lv | sepc.all | sepc.nox |
|---|---|---|---|---|---|---|---|
| exercise | ~ | PBC | 90.14 | 7.601 | 7.049 | 0.3695 | 0.3695 |
| PBC | ~ | exercise | 89.49 | 0.04938 | 0.05325 | 1.016 | 1.016 |
Of these suggested paths, the largest MI is for the one which says PBC is predicted by exercise. However, the model would also be improved by allowing PBC to predict exercise. Which should we add?
The answer will depend on both previous theory and knowledge of the data.
If it were the case that exercise was measured at a later time point than PBC. In this case the decision is reasonably clear, because the temporal sequencing of observations would determine the most likely path. These data were collected contemporaneously, however, and so we can’t use our design to differentiate the causal possibilities.
Another consideration would be that, by adding a path from exercise to PBC we would make the model non-recursive, and likely non-identified.
A theorist might also argue that because previous studies, and the theory of planned behaviour itself, predict that PBC may exert a direct influence on behaviour, we should add the path with the smaller MI (so allow PBC to predict exercise).
In this case, the best course of action would probably be to report the theoretically implied model, but also test alternative models in which causal relations between the variables are reversed or otherwise altered (along with measures of fit and key parameter estimates). The discussion of your paper would then make the case for your preferred account, but make clear that the data were (most likely) unable to provide a persuasive case either way, and that alternative explanations cannot be ruled out.
Interpreting and presenting key parameters
One of the best ways to present estimates from your final model is in a diagram, because this is intutive and provides a simple way for readers to comprehend the paths implied by your model.
We can automatically generate a plot from a fitted model using semPaths().
Here, the what='std' is requesting standardised parameter estimates be shown.
Adding residuals=F hides variances of observed and latent variables, which are
not of interest here. The line thicknesses are scaled to represent the size
parameter itself:
semPlot::semPaths(sem.mod.fit, what='std', residuals=F)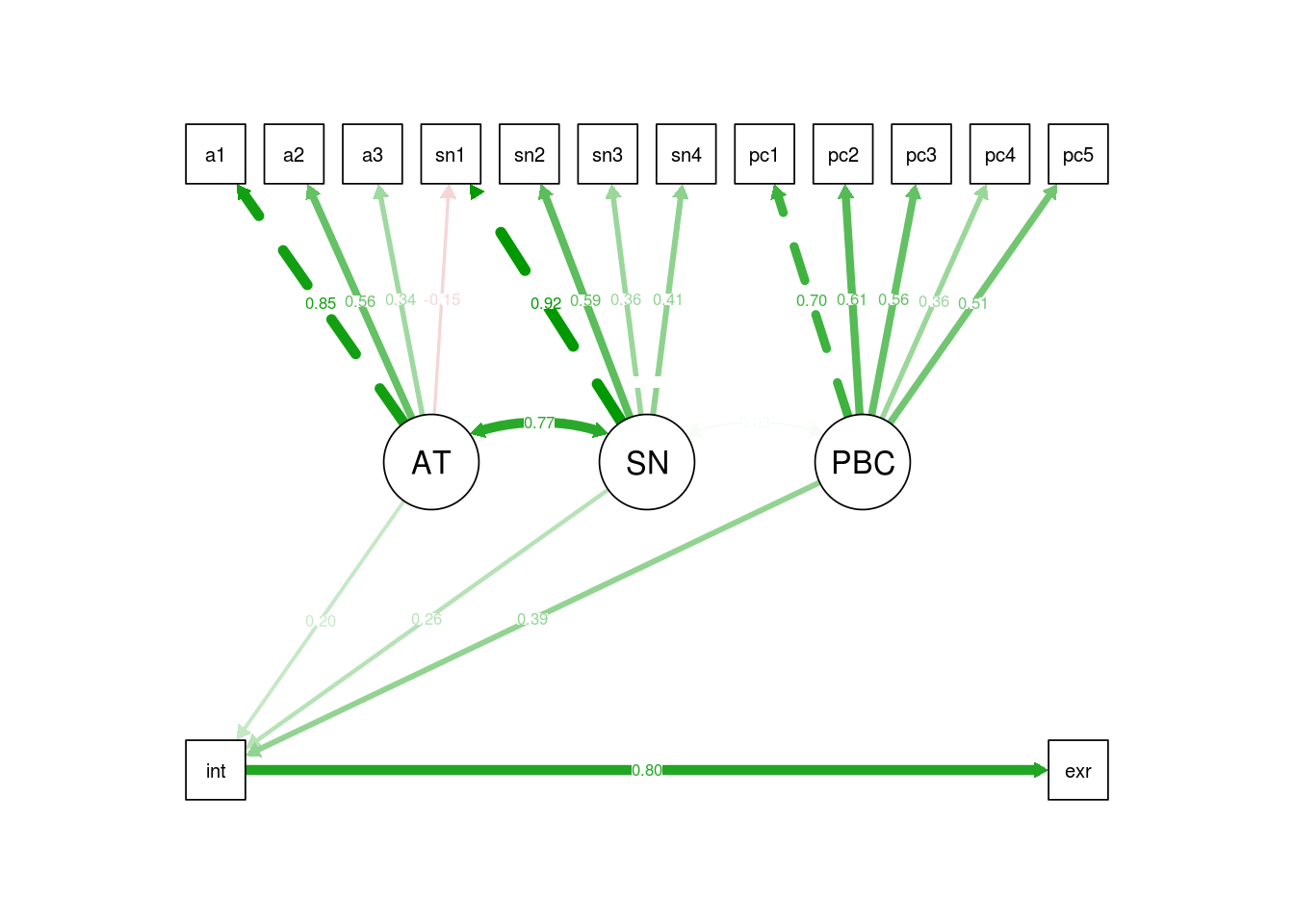
For more information on reporting SEM however, see @schreiber2006reporting.