Mediation

Mediation is a complex topic, and the key message to take on — before starting to analyse your data — is that mediation analayses make many strong assumptions abou the data. These assumptions can often be pretty unreasonable, when spelled out, so be cautious in the interpretation of you data.

Put differently, mediation is a correlational technique aiming to provide a causal interpretation of data; caveat emptor.

Mediation with multiple regression

One common (if outdated) way to analyse mediation is via the 3 steps described by Baron and Kenny @baron1986moderator (also see @zhao_reconsidering_2010).

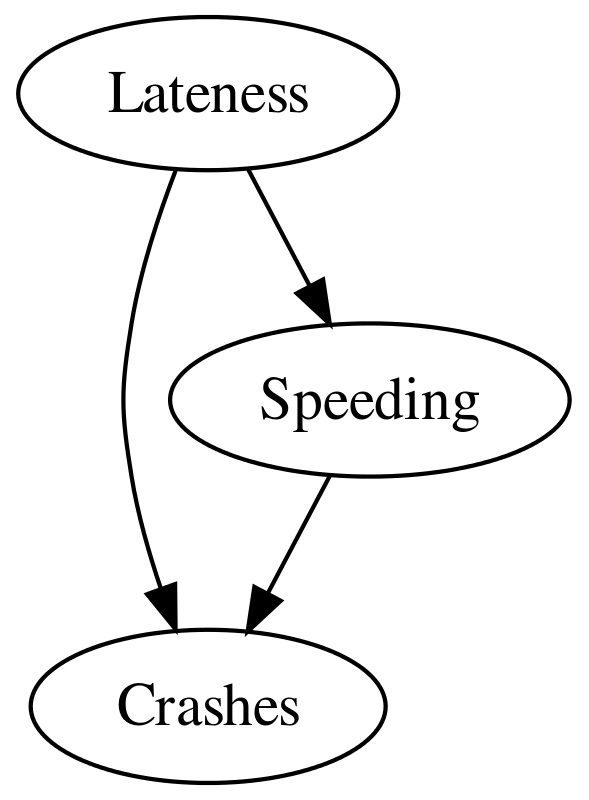
Let’s say we have a hypothesised situation such as this:

knit_gv("
Lateness -> Crashes
Lateness -> Speeding
Speeding -> Crashes
")

Baron and Kenny propose 3 steps to establishing mediation. These steps correspond to three separate regression models:

Mediation Steps

Step 1 (check distal variable predicts mediator)

That is, show Lateness predicts Crashes

Step 2 (check distal variable predict mediator)

That is, show Lateness predicts Speeding

Step 3 (check for mediation)

That is, show Speeding predicts Crashes, controlling for Lateness

An additional step, which allows us to test whether the effect is completely mediated, also uses the final regression model:

Step 4 (check for total mediation)

That is, check if Lateness still predicts crashes, controlling for Lateness

Mediation example after Baron and Kenny

Using simulated data, we can work through the steps.

smash %>% glimpse
Observations: 200
Variables: 4
$ person   <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, …
$ lateness <int> 11, 12, 9, 8, 11, 4, 11, 7, 8, 11, 9, 10, 9, 11, 13, 10…
$ speed    <dbl> 48.88524, 43.07030, 33.72812, 44.17897, 51.22378, 40.86…
$ crashes  <int> 15, 9, 12, 20, 25, 13, 22, 14, 22, 18, 11, 16, 19, 15, …

Step 1: does lateness predict crashes?

step1 <- lm(crashes ~ lateness, data=smash)
tidy(step1) %>% pander()

term	estimate	std.error	statistic	p.value
(Intercept)	12.15	1.204	10.09	1.365e-19
lateness	0.4448	0.1125	3.953	0.0001074

Step 2: Does lateness predict speed?

step2 <- lm(speed ~ lateness, data=smash)
tidy(step2, conf.int = T) %>% pander()

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	33.42	2.275	14.69	1.563e-33	28.93	37.9
lateness	0.515	0.2126	2.422	0.01633	0.09573	0.9343

The coefficient for lateness is statistically significant, so we would say yes.

Step 3: Does speed predict crashes, controlling for lateness?

step3 <- lm(crashes ~ lateness+speed, data=smash)
tidy(step3) %>% pander()

term	estimate	std.error	statistic	p.value
(Intercept)	2.542	1.465	1.735	0.08427
lateness	0.2967	0.09611	3.088	0.002309
speed	0.2875	0.03166	9.083	1.122e-16

The coefficient for speed is statistically significant, so we can say mediation does occur.

Step 4: In the same model, does lateness predict crashes, controlling for speed? That is to say, is the mediation via speed total?

Here, the coefficient is still statistically significant. According to the Baron and Kenny steps, this would indicate the mediation is partial, although the fact the p value falls one side or another of .05 is not necessarily the best way to express this (see below for ways to calculate the proportion of the effect which is mediated).

We should alse be concerned here with the degree to which predictor and mediator are measured with error — if they are noisy measures, then the proportion of the effect which appears to be mediated will be reduced artificially (see the SEM chapter for more on this).